Question

A Randstad/Harris interactive survey reported that 25% of employees said their company is loyal to them. Suppose 9 employees are selected randomly and will be interviewed about company loyalty.

A. What is the probability that none of the 9 employees will say their company is loyal to them?

c. What is the probability that 4 of the 9 employees will say their company is loyal to them?

Answer 1

(A) 0.999996

(B) 0.11680

Explanation:

We are given that a Randstad Harris interactive survey reported that 25% of employees said their company is loyal to them.

And 9 employees are selected randomly and interviewed about company loyalty.

The Binomial probability distribution is given by;

`P(X=r)= \binom{n}{r}p^(r)(1-p)^(n-r) for x = 0,1,2,3,....`

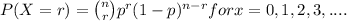
where, n = number of trials (samples) taken

r = number of success

p = probability of success

In our question; n = 9 , p = 0.25 (as employees saying their company is loyal to them is success to us)

(A) Probability that none of the 9 employees will say their company is loyal to them = 1 - Probability that all 9 employees will say their company is loyal to them

= 1 - P(X = 9) { As here number of success is 9 }

= 1 -
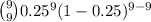`\binom{9}{9}0.25^(9)(1-0.25)^(9-9)` = 1 -
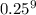`0.25^(9)` = 0.999996

(B) Probability that 4 of the 9 employees will say their company is loyal to them = P(X = 4)

P(X = 4) =
`\binom{9}{4}0.25^(4)(1-0.25)^(9-4)`

=
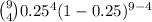
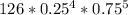`126*0.25^(4)*0.75^(5)` = 0.11680