Question

You're driving a vehicle of mass 1350 kg and you need to make a turn on a flat road. The radius of curvature of the turn is 71 m. The maximum horizontal component of the force that the road can exert on the tires is only 0.23 times the vertical component of the force of the road on the tires (in this case the vertical component of the force of the road on the tires is mg, the weight of the car, where as usual g = +9.8 N/kg, the magnitude of the gravitational field near the surface of the Earth). The factor 0.23 is called the "coefficient of friction" (usually written "", Greek "mu") and is large for surfaces with high friction, small for surfaces with low friction.

(a) What is the fastest speed you can drive and still make it around the turn? Invent symbols for the various quantities and solve algebraically before plugging in numbers.
maximum speed =_______________ m/s

Answer 1

`v=12.65\ m.s^(-1)`

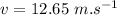
Step-by-step explanation:

Given:

• mass of vehicle,
  `m=1350\ kg`

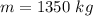
• radius of curvature,
  `r=71\ m`

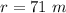
• coefficient of friction,
  `\mu=0.23`

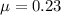
During the turn to prevent the skidding of the vehicle its centripetal force must be equal to the opposite balancing frictional force:

`m.(v^2)/(r) =\mu.N`

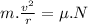
where:

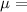`\mu=` coefficient of friction

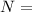`N=` normal reaction force due to weight of the car

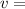`v=` velocity of the car

`1350* (v^2)/(71) =0.23* (1350* 9.8)`

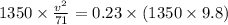
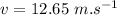`v=12.65\ m.s^(-1)` is the maximum velocity at which the vehicle can turn without skidding.