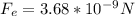Question

In the Rutherford model of hydrogen the electron (mass=9.11x10-31 kg) is in a planetary type orbit around the proton (mass=1.67x10-27 kg). Assume that the radius of the orbit is 2.5 Angstroms (10-10 m). (a) What is the magnitude of the gravitational force of attraction between electron and proton? AN (b) What is the magnitude of the electric force of attraction between electron and proton? N

Answer 1

(a)
`F_g=1.62*10^(-48)N`

(b)
`F_e=3.68*10^(-9)N`

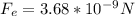
Step-by-step explanation:

(a) We use Newton's law of universal gravitation, in order to calculate the gravitational force between electron and proton:

`F_g=-G(m_1m_2)/(r^2)`

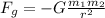
Where G is the Cavendish gravitational constant,
`m_1` and
`m_2` are the masses of the electron and the proton respectively and r is the distance between them:

`F_g=-6.67*10^(-11)(N\cdot m^2)/(kg^2)((9.11*10^(-31)kg)(1.67*10^(-27)kg))/((2.5*10^(-10)m)^2)\\F_g=-1.62*10^(-48)N`

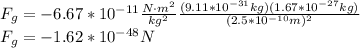
The minus sing indicates that the force is repulsive. Thus, its magnitude is:

`F_g=1.62*10^(-48)N`

(b) We use Coulomb's law, in order to calculate the electric force between electron and proton, here k is the Coulomb constant and e is the elementary charge:

`F_e=-k(e^2)/(r^2)\\F_e=-8.99*10^(9)(N\cdot m^2)/(C^2)((1.6*10^(-19)C)^2)/((2.5*10^(-10)m)^2)\\F_e=-3.68*10^(-9)N`

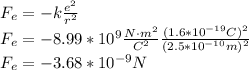
Its magnitude is:

`F_e=3.68*10^(-9)N`