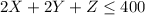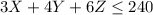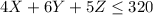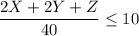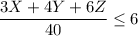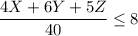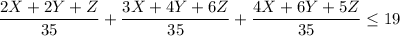Question

Each machine must be run by one of 19 cross-trained workers who are each available 35 hours per week. The plant has 10 type 1 machines available, 6 type 2 machines available, and 8 type 3 machines available. Products 1, 2, and 3 contribute $90, $120, and $150, respectively, in marginal profit per unit produced.

Answer 1

The Linear programming model is given as below

Profit Function:
`P=90X+120Y+150Z`

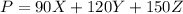
Constraints:

`2X+2Y+Z\leq 400`

`3X+4Y+6Z\leq 240`

`4X+6Y+5Z\leq 320`

`(2X+2Y+Z)/(40)\leq 10`

`(3X+4Y+6Z)/(40)\leq 6`

`(4X+6Y+5Z)/(40)\leq 8`

`(2X+2Y+Z)/(35)+(3X+4Y+6Z)/(35)+(4X+6Y+5Z)/(35)\leq 19`

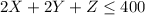
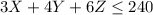
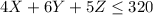
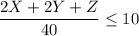
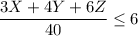
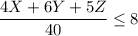
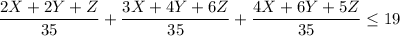
Step-by-step explanation:

As the question is not complete, the complete question is found online and is attached herewith.

Let the number of product 1 to be produced is X, that of product 2 is Y and product 3 is Z

so the maximizing function is the profit function which is given as

`P=90X+120Y+150Z`

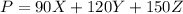
Now as the number of hours in a week are 40 and there are a total of 10 type 1 machines so the total number of machine 1 hours are 40*10=400 hours

As from the given table product 1 uses 2 machine hours of machine 1, product 2 uses 2 machine hours of machine 1 and product 3 uses 1 hour of machine 1 so

`2X+2Y+Z\leq 400`

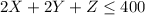
Now as the number of hours in a week are 40 and there are a total of 6 type 2 machines so the total number of machine 2 hours are 40*6=240 hours

As from the given table product 1 uses 3 machine hours of machine 2, product 2 uses 4 machine hours of machine 2 and product 3 uses 6 hour of machine 2 so

`3X+4Y+6Z\leq 240`

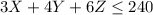
Now as the number of hours in a week are 40 and there are a total of 8 type 3 machines so the total number of machine 3 hours are 40*8=320 hours

As from the given table product 1 uses 4 machine hours of machine 3, product 2 uses 6 machine hours of machine 3 and product 3 uses 5 hour of machine 3 so

`4X+6Y+5Z\leq 320`

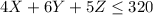
Now as the machine 1 is used as 2X+2Y+Z in a week and the week is of 40 hours so the number of machines to be used are given as

`(2X+2Y+Z)/(40)\leq 10`

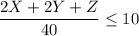
Now as the machine 2 is used as 3X+4Y+6Z in a week and the week is of 40 hours so the number of machines to be used are given as

`(3X+4Y+6Z)/(40)\leq 6`

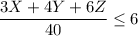
Now as the machine 3 is used as 4X+6Y+5Z in a week and the week is of 40 hours so the number of machines to be used are given as

`(4X+6Y+5Z)/(40)\leq 8`

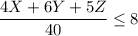
Now the workers are available for 35 hours so the worker available at the machine 1 is given as

`(2X+2Y+Z)/(35)`

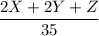
That of machine 2 is given as

`(3X+4Y+6Z)/(35)`

That of machine 3 is given as

`(4X+6Y+5Z)/(35)`

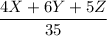
As the total number of workers is 19 so the constraint is given as

`(2X+2Y+Z)/(35)+(3X+4Y+6Z)/(35)+(4X+6Y+5Z)/(35)\leq 19`

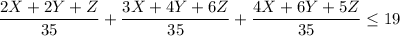
So the Linear programming model is given as below

Profit Function:
`P=90X+120Y+150Z`

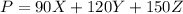
Constraints:

`2X+2Y+Z\leq 400`

`3X+4Y+6Z\leq 240`

`4X+6Y+5Z\leq 320`

`(2X+2Y+Z)/(40)\leq 10`

`(3X+4Y+6Z)/(40)\leq 6`

`(4X+6Y+5Z)/(40)\leq 8`

`(2X+2Y+Z)/(35)+(3X+4Y+6Z)/(35)+(4X+6Y+5Z)/(35)\leq 19`