Question

How much further up the wall does the ladder in figure 2 reach than

the ladder in figure 1 (to the nearest tenth of a foot)?

Answer 1

Answer: the answer is 3.2 when rounded

Step-by-step explanation:

if you want the explanation look at the one above

Answer 2

The ladder in figure 2 reaches 3.2 feet further up than the ladder in figure 1.

Explanation:

Step 1:

In both the given figures, the ladder, the wall and the floor form a right-angled triangle. The floor is the adjacent side, the wall is the opposite side and the ladder is the hypotenuse.

According to the Pythagorean theorem,

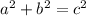`a^(2)+b^(2)=c^(2)`, where c is the length of the hypotenuse while a and b are the lengths of the other two sides.

Step 2:

For the ladder in figure 1, assume the distance from the floor to the ladder's top is x feet. So a = x, b = 8 and c = 10 (hypotenuse).

`a^(2)+b^(2)=c^(2)`,
`x^(2)+8^(2)=10^(2)`,
`x^(2)=100-64=36, x=√(36)=6 \text { feet }`.

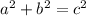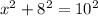So the distance between the floor and the ladder's top is 6 feet.

Step 3:

For the ladder in figure 2, assume the distance between the floor and the ladder's top is y feet. So a = y, b = 4 and c = 10 (hypotenuse).

`a^(2)+b^(2)=c^(2)`,
`y^(2)+4^(2)=10^(2)`,
`y^(2)=100-16=48, x=√(84)=9.1651 \text { feet }`.

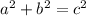So the distance between the floor and the ladder's top is 9.1651 feet.

Step 4:

The difference in heights = The wall height in figure 2 - the wall height in figure 1.

The difference in heights = 9.1651 feet - 6 feet = 3.1651 feet.

Rounding this off to the nearest tenth of a foot, we get 3.2 feet.