Question

Montoya (2007) asked 56 men and 82 women to rate 21 different body parts on a scale of 1 (no opinion) to 5 (very desirable). They found that men and women rated the eyes similarly, with an average rating of about 3.77 ± 1.23 (M ± SD). Assuming these data are normally distributed, answer the following questions. (Round your answers to two decimal places.) (a) What percentage of participants rated the eyes at least a 5 (very desirable)? % (b) What percentage rated the eyes at most a 1 (no opinion)? %

Answer 1

a. 15.9%

b. 1.2%

Explanation:

using the normal distribution we have the following expression

`P(X\geq a)=P((X-u)/(\alpha ) \geq (5-M)/(SD)) \\`

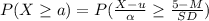
Where the first expression in the right hand side is the z-scores, M is the mean of value 3.77 and SD is the standard deviation of value 1.23.

if we simplify and substitute values, we arrive at

`P(X\geq a)=P((X-u)/(\alpha ) \geq (a-M)/(SD)) \\P(X\geq 5)=P(Z \geq (5-3.77)/(1.23))\\P(X\geq 5)=P(Z \geq 1)\\P(X\geq 5)=1- P(Z < 5)\\P(X\geq 5)=1-0.841\\P(X\geq 5)=0.159`

in percentage, we arrive at 15.9%

b. for the percentage rated the eyes most a 1

`P(X\leq a)=P((X-u)/(\alpha ) \leq (a-M)/(SD))\\for a=1\\P(X\leq 1)=P(Z \leq (1-3.77)/(1.23))\\P(X\leq 1)=P(Z \leq -2.25})\\P(X\leq 1)=0.012\\`

In percentage we have 1.2%