Question

The circuit to the right consists of a battery ( V 0 = 64.5 V) (V0=64.5 V) and five resistors ( R 1 = 711 (R1=711 Ω, R 2 = 182 R2=182 Ω, R 3 = 663 R3=663 Ω, R 4 = 534 R4=534 Ω, and R 5 = 265 R5=265 Ω). Find the current passing through each of the specified points. -g

Answer 1

The current in R₁ is 0.0816 A.

The current at H point is 0.0243 A.

Explanation:

Given that,

Voltage = 64.5

Resistance is

`R_(1)=711\ \Omega`

`R_(2)=182\ \Omega`

`R_(3)=663\ \Omega`

`R_(4)=534\ \Omega`

`R_(5)=265\ \Omega`

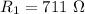
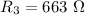
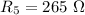
Suppose, The specified points are R₁ and H.

According to figure,

R₂,R₃,R₄ and R₅ are connected in parallel

We need to calculate the resistance

Using parallel formula

`(1)/(R)=(1)/(R_(2))+(1)/(R_(3))+(1)/(R_(4))+(1)/(R_(5))`

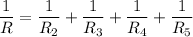
Put the value into the formula

`(1)/(R)=(1)/(182)+(1)/(663)+(1)/(534)+(1)/(265)`

`(1)/(R)=(35501)/(2806615)`

`R=79.05\ \Omega`

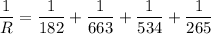
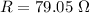
R and R₁ are connected in series

We need to calculate the equilibrium resistance

Using series formula

`R_(eq)=R_(1)+R`

`R_(eq)=711+79.05`

`R_(eq)=790.05\ \Omega`

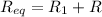
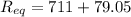
We need to calculate the equivalent current

Using ohm's law

`i_(eq)=(V)/(R_(eq))`

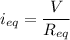
Put the value into the formula

`i_(eq)=(64.5)/(790.05)`

`i_(eq)=0.0816\ A`

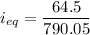
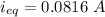
We know that,

In series combination current distribution in each resistor will be same.

So, Current in R and R₁ will be equal to
`i_(eq)`.

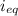The current at h point will be equal to current in R₅

We need to calculate the voltage in R

Using ohm's law

`V=I_(eq)*R`

Put the value into the formula

`V=0.0816*79.05`

`V=6.45\ Volt`

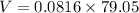
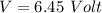
In resistors parallel combination voltage distribution in each part will be same.

So,
`V_(2)=V_(3)=V_(4)=V_(5)=6.45 V`

We need to calculate the current at H point

Using ohm's law

`i_(h)=(V_(5))/(R_(5))`

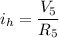
Put the value into the formula

`i_(h)=(6.45)/(265)`

`i_(h)=0.0243\ A`

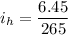
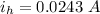
Hence, The current in R₁ is 0.0816 A.

The current at H point is 0.0243 A.