Answer:
The lowest possible frequency of sound is 971.4 Hz.
Step-by-step explanation:
Given that,
Distance between loudspeakers = 2.00 m
Height = 5.50 m
Sound speed = 340 m/s
We need to calculate the distance
Using Pythagorean theorem
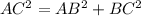
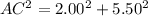
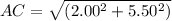
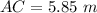
We need to calculate the path difference
Using formula of path difference
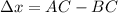
Put the value into the formula
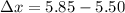

We need to calculate the lowest possible frequency of sound
Using formula of frequency

Put the value into the formula
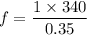
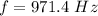
Hence, The lowest possible frequency of sound is 971.4 Hz.