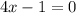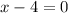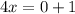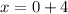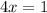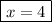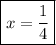Answer:
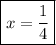 and
and
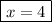
Explanation:
Given equation:
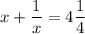
Step-1: Convert the mixed fraction on the R.H.S into improper fraction
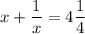
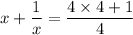
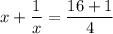
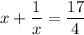
Step-2: Make common denominators on the L.H.S:
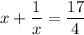
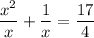
Step-3: Combine the denominators on the L.H.S
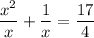
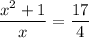
Step-4: Use cross multiplication
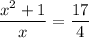
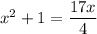
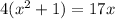
Step-5: Simplify the distributive property
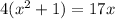
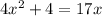
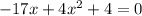
Step-6: Change "-17x" to "-16x - x" as it is equivalent
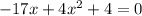
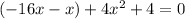
Step-7: Factor the common terms
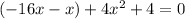
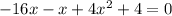
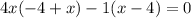
Step-8: Group the terms
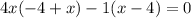
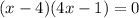
Step-9i: Use cross multiplication for (x - 4)
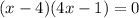
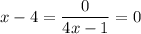
Step-9ii: Use cross multiplication for (4x - 1)
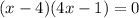
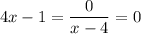
Thus
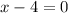 and
and
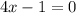 .
.
Step-10: Simplify both equations