Question

A study of the checkout lines at the Safeway Supermarket in the South Strand area revealed that between 4 and 7 P.M. on weekdays there is an average of four customers waiting in line. What is the probability that you visit Safeway today during this period and find?

a. No customers are waiting?
b. Four customers are waiting?
c. Four or fewer are waiting?
d. Four or more are waiting?

Answer 1

(a) The probability of no customers are waiting in a line is 0.01832.

(b) The probability of 4 customers are waiting in a line is 0.19537.

(c) The probability of 4 or fewer customers are waiting in a line is 0.62885.

(d) The probability of 4 or more customers are waiting in a line during the visit is 0.56652.

Explanation:

The number of customers waiting in a line between 4 PM and 7 PM (X) follows a Poisson distribution with parameter λ = 4.

The probability mass function of a Poisson distribution is:

`P(X=x)=(e^(-4)(4)^(x))/(x!) ;\ x=0, 1, 2,...`

(a)

Compute the probability that no customers are waiting in a line during the visit as follows:

`P(X=0)=(e^(-4)(4)^(0))/(0!)=(0.01832*1)/(1)=0.01832`

Thus, the probability of no customers are waiting in a line is 0.01832.

(b)

Compute the probability that 4 customers are waiting in a line during the visit as follows:

`P(X=4)=(e^(-4)(4)^(4))/(4!)=(0.01832*256)/(24)=0.19537`

Thus, the probability of 4 customers are waiting in a line is 0.19537.

(c)

Compute the probability that 4 or fewer customers are waiting in a line during the visit as follows:

P (X ≤ 4) = P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4)

`=(e^(-4)(4)^(0))/(0!)+(e^(-4)(4)^(1))/(1!)+(e^(-4)(4)^(2))/(2!)+(e^(-4)(4)^(3))/(3!)+(e^(-4)(4)^(3))/(3!)+(e^(-4)(4)^(4))/(4!)\\=0.01832+0.07326+0.14653+0.19537+0.19537\\=0.62885`

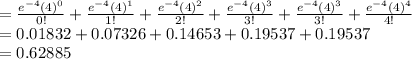
Thus, the probability of 4 or fewer customers are waiting in a line is 0.62885.

(d)

Compute the probability of 4 or more customers are waiting in a line during the visit as follows:

P (X ≥ 4) = 1 - P (X < 4)

= 1 - P (X = 0) - P (X = 1) - P (X = 2) - P (X = 3)

`=1-(e^(-4)(4)^(0))/(0!)+(e^(-4)(4)^(1))/(1!)+(e^(-4)(4)^(2))/(2!)+(e^(-4)(4)^(3))/(3!)+(e^(-4)(4)^(3))/(3!)\\=1-0.01832-0.07326-0.14653-0.19537\\=0.56652`

Thus, the probability of 4 or more customers are waiting in a line during the visit is 0.56652.