Answer:
- The maximum height is 136 ft
- The time it takes to achieve this height is 1.5 s.
Step-by-step explanation:
1. Function for the height (given):
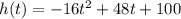
2. Type of function
That is a quadatic function, whose graph is a parabola that opens downward.
The maximum of the function, i.e. the maximum height, is the vertex of the parabola.
The vertex of a parabola with the genral equation
 is at the x-coordinate
is at the x-coordinate
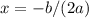
3. Time to achieve the maximum height
Substitute b with 48 and a with - 16:
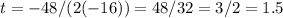
Then, time when the object achieves the maximum height it 1.5s
4. Maximum height:
Replace t with 1.5 in the equation, to find the maximum height, h(1.5)
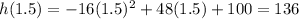
Then, the maximum height is 136 ft