Answer with Explanation:
We are given that
Diameter of coil=d=0.115mm
Radius, r=
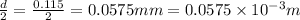
Using
Electric field=E=0.235V/m
T=55 degree C
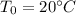
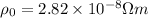
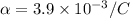
(a).We know that
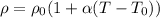
Substitute the values
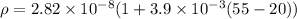
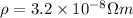
(b).Current density,

Using the formula
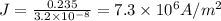
c.Total current,I=JA
Where
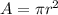
Using the formula

I=0.076A
d.Length of wire=l=2m
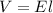
Substitute the values
