Question

Determine the longest interval in which the given initial value problem is certain to have a unique twice-differentiable solution. Do not attempt to find the solution. (Enter your answer using interval notation.) ty'' + 7y = t, y(1) = 1, y'(1) = 7

Answer 1

The longest interval in which the given initial value problem is certain to have a unique twice-differentiable solution is (0,∞)

Explanation:

Given the differential equation:

ty'' + 7y = t .................................(1)

Together with the initial conditions:

y(1) = 1, y'(1) = 7

We want to determine the longest interval in which the given initial value problem is certain to have a unique twice-differentiable solution.

First, let us have the differential equation (1) in the form:

y'' + p(t)y' + q(t)y = r(t) ..................(2)

We do that by dividing (1) by t

So that

y''+ (7/t)y = 1 ....................................(3)

Comparing (3) with (2)

p(t) = 0

q(t) = 7/t

r(t) = 1

For t = 0, p(t) and r(t) are continuous, but q(t) = 7/0, which is undefined. Zero is certainly out of the required points.

In fact (-∞, 0) and (0,∞) are the points where p(t), q(t) and r(t) are continuous. But t = 1, which is contained in the initial conditions is found in (0,∞), and that makes it the correct interval.

So the largest interval containing 1 on which p(t), q(t) and r(t) are defined and continuous is (0,∞)

Answer 2

`y'' + (7)/(t) y = 1`

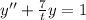
For this case we can use the theorem of Existence and uniqueness that says:

Let p(t) , q(t) and g(t) be continuous on [a,b] then the differential equation given by:

`y''+ p(t) y' +q(t) y = g(t) , y(t_o) =y_o, y'(t_o) = y'_o`

has unique solution defined for all t in [a,b]

If we apply this to our equation we have that p(t) =0 and
`q(t) = (7)/(t)` and
`g(t) =1`

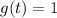
We see that
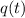`q(t)` is not defined at t =0, so the largest interval containing 1 on which p,q and g are defined and continuous is given by
`(0, \infty)`

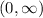
And by the theorem explained before we ensure the existence and uniqueness on this interval of a solution (unique) who satisfy the conditions required.

Explanation:

For this case we have the following differential equation given:

`t y'' + 7y = t`

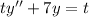
With the conditions y(1)= 1 and y'(1) = 7

The frist step on this case is divide both sides of the differential equation by t and we got:

`y'' + (7)/(t) y = 1`

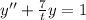
For this case we can use the theorem of Existence and uniqueness that says:

Let p(t) , q(t) and g(t) be continuous on [a,b] then the differential equation given by:

`y''+ p(t) y' +q(t) y = g(t) , y(t_o) =y_o, y'(t_o) = y'_o`

has unique solution defined for all t in [a,b]

If we apply this to our equation we have that p(t) =0 and
`q(t) = (7)/(t)` and
`g(t) =1`

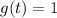
We see that
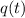`q(t)` is not defined at t =0, so the largest interval containing 1 on which p,q and g are defined and continuous is given by
`(0, \infty)`

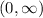
And by the theorem explained before we ensure the existence and uniqueness on this interval of a solution (unique) who satisfy the conditions required.