Question

Calculate the magnitude and direction (i.e., the angle with respect to the positive H-axis, measured positive as counter-clockwise) of the total force acting on M. Notice that the arrows representing the forces end on grid intersections.

Answer 1

The graphics in the attachment is part of the question, which was incomplete.

Answer: Fr = 102N and angle of approximately 11°.

Explanation: From the attachment, it is observed that from the three forces acting on M, two are perpendicular. So to find them, we have to show their x- and y- axis components. From the graph:

Fx = 70+40-10 = 100

Fy = 40-20 = 20

Now, as the forces form a triangle, the totalforce is:

Fr =
`\sqrt{Fx^(2) +Fy^(2) }`

Fr =
`√(10400)`

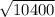
Fr = ≈ 102N

To determine the angle requested, we use:

arctg H =
`(Fy)/(Fx)`

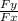
arctg H =
`(20)/(100)`

H = tg 0.2 ≈ 11°.