Answer:
No, these functions fail to be inverses of each other.
Explanation:
We have two functions :
- f(x) = 3x + 2
- g(x) =
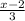
Let's take the function f(x) and take x = 1.
- f(1) = 3(1) + 2
- f(1) = 5 [Keep this in mind]
- If f(1) is 5, then if g(x) is an inverse function, g(1) should be
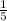
Let's try the same with g(x).
- g(1) =
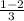
- g(1) =
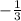
Clearly, they are not inverse functions of each other.