Question

Calculate the force required to pull a copper ball of radius 1.69 cm upward through a viscous fluid at a constant speed of 9.3 cm/s. Take the damping constant of the fluid to be 0.884 kg/s\.\*

Answer 1

`m = \rho V`

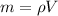
Since we have an ball we can consider this like a sphere and the volume is given by
`V = (4)/(3) \pi r^3 = (4)/(3) \pi (1.69cm)^3 = 20.218 cm^3 = 0.00002022 m^3`

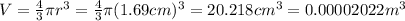
The density for the copper is approximately
`\rho = 8940 kg/m^3`

So then the mass is :

`m =8940 kg/m^3 * 0.00002022m^3 = 0.1808 Kg`

And now we have everything in order to replace into the formula for F, like this:
`F = 0.1808 Kg *9.8 m/s^2 + 0.884 kg/s * 0.093 m/s= 1.772 +0.975 N = 2.747 N`And that would be the final answer for this case.

Step-by-step explanation:

For this case if we assume that we have a damping motion the force action on the vertical direction would be:

`F = mg + bv`

Where F represent the upward force on the copper ball

m represent the mass

g = 9.8 m/s^2 represent the gravity

b = 0.884 kg/s represent the proportionality constant

v = 9.3 cm/s = 0.093 m/s represent the velocity

We can solve for the mass from the following expression:

`m = \rho V`

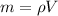
Since we have an ball we can consider this like a sphere and the volume is given by
`V = (4)/(3) \pi r^3 = (4)/(3) \pi (1.69cm)^3 = 20.218 cm^3 = 0.00002022 m^3`

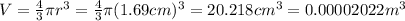
The density for the copper is approximately
`\rho = 8940 kg/m^3`

So then the mass is :

`m =8940 kg/m^3 * 0.00002022m^3 = 0.1808 Kg`

And now we have everything in order to replace into the formula for F, like this:
`F = 0.1808 Kg *9.8 m/s^2 + 0.884 kg/s * 0.093 m/s= 1.772 +0.975 N = 2.747 N`And that would be the final answer for this case.