Step-by-step explanation:
Here we know that the linearized regression equation for an exponential data set is:

Where:
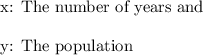
The predicted population when
 is found by substituting this value into the equation and finding
is found by substituting this value into the equation and finding
 :
:
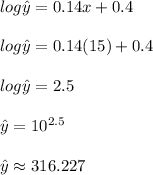
Since population is a natural number, we must round off, therefore, the predicted population is 316, option C.