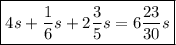Question

Simplify by combining like terms 4s + 1/6s + 2 3/5s. There’s supposed to be a whole number and a fraction for the answer. Please HELP!

Answer 1

`6(23)/(30) s`

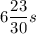
Explanation:

The first step in simplying

`$4s+(1)/(6)s +2(3)/(5)s $`

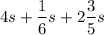
is to bring the mixed number
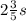`2(3)/(5)s` into the form of an improper fraction:

`$2(3)/(5)s = (2+(3)/(5))s =((10)/(5) +(3)/(5))s = (13)/(5)s $`

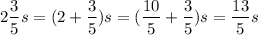
Therefore, the expression now becomes

`$4s+(1)/(6)s +(13)/(5)s $`

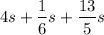
and to simplify further we find the common denominator of the fractions which is

`6*5 =30`,

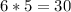therefore,

`$4s+(5)/(30)s +(78)/(30)s $`

`$(120)/(30) s+(5)/(30)s +(78)/(30)s $`

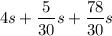
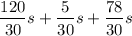
add the numerator and get:

`(203)/(30) s`

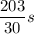
as a mixed number this is

`6(23)/(30) s`

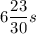
Thus,

`$\boxed{4s+(1)/(6)s +2(3)/(5)s = 6(23)/(30) s} $`