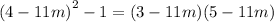Answer
a)
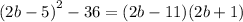
b)
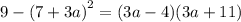
c)
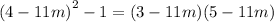
Step-by-step explanation
a) The given expresion is
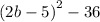
We rewrite as difference of two squares
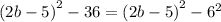
Recall that:
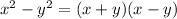
This implies that:
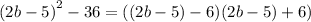
Or
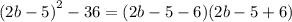
This simplifies to give:
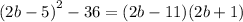
b) The second expression is
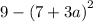
We rewrite as perfect squares yo get:
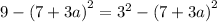
This gives:
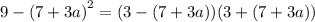
This implies that
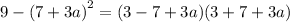
We simplify to get:
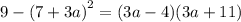
c) The third expression is:
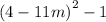
We obtain the difference of two squares as:
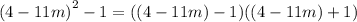
We simplify within the parenthesis to get:
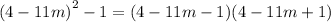
We simplify further to get;