Question

A manufacturer of nickel-hydrogen batteries randomly selects 100 nickel plates for test cells, cycles them a specified number of times and determines that 14 of the plates have blistered.

Does this data provide compelling evidence for concluding that more than 10% of all plates blister under such circumstances?

Use Alpha =0.10.

A. What is the parameter of interest?

B. State the null and alternative hypotheses.

C. Calculate the test statistic.

D. Find the rejection region.

E. Make a decision and interpret.

F. Find a p-value corresponding to the test and compare with your decision in E.

Answer 1

a) Parameter of interest
`p` representing the true proportion of the plates have blistered.

b) Null hypothesis:
`p\leq 0.1`

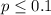
Alternative hypothesis:
`p > 0.1`

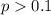
c)
`z=\frac{0.14 -0.1}{\sqrt{(0.1(1-0.1))/(100)}}=1.33`

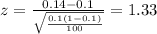
d) For this case we need to find a value in the normal standard distribution that accumulates 0.1 of the area in the right tail and for this case is:

`z_(critc)= 1.28`

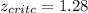
e) For this case since our calculated value is higher than the critical value 1.33>1.28 we have enough evidence to reject the null hypothesis and we can conclude that the true proportion is significantly higher than 0.1

f)
`p_v =P(z>1.33)=0.0917`

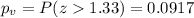
If we compare the p value and the significance level given
`\alpha=0.1` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 10% of significance the true proportion is higher than 0.1 or 10%

Explanation:

Data given and notation

n=100 represent the random sample taken

Part a

Parameter of interest
`p` representing the true proportion of the plates have blistered.

X=14 represent the number of the plates have blistered.

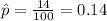`\hat p=(14)/(100)=0.14` estimated proportion of the plates have blistered.

`p_o=0.1` is the value that we want to test

`\alpha=0.1` represent the significance level

Confidence=90% or 0.90

z would represent the statistic (variable of interest)

`p_v` represent the p value (variable of interest)

Part b: Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that more than 10% of all plates blister under such circumstances.:

Null hypothesis:
`p\leq 0.1`

Alternative hypothesis:
`p > 0.1`

When we conduct a proportion test we need to use the z statistic, and the is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
`\hat p` is significantly different from a hypothesized value
`p_o`.

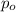Part c: Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.14 -0.1}{\sqrt{(0.1(1-0.1))/(100)}}=1.33`

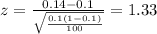
Part d: Rejection region

For this case we need to find a value in the normal standard distribution that accumulates 0.1 of the area in the right tail and for this case is:

`z_(critc)= 1.28`

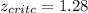
Part e

For this case since our calculated value is higher than the critical value 1.33>1.28 we have enough evidence to reject the null hypothesis and we can conclude that the true proportion is significantly higher than 0.1

Part f

Since is a right taild test the p value would be:

`p_v =P(z>1.33)=0.0917`

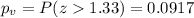
If we compare the p value and the significance level given
`\alpha=0.1` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can said that at 10% of significance the true proportion is higher than 0.1 or 10%