Question

Rewrite the equation by completing the square.

2 x^{2} -9 x +7 = 0

(x+blank )^2=blank

Answer 1

`(x+ -(9)/(4) )^(2) = (25)/(16)`

Khan

Answer 2

Rewrite the equation by completing the square:

`(2x + 9)^2 = (53)/(4)`

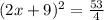
Solution:

Given that,

`2x^2 - 9x + 7 = 0`

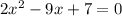
We have to rewrite by completing the square

Step 1:

The general quadratic equation is given as:

`ax^2 + bx + c = 0`

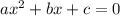
Compare with given, we get,

a = 2

b = -9

c = 7

Step 2:

From given,

`2x^2 - 9x + 7 = 0`

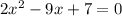
Subtract 7 from both sides,

`2x^2 - 9x = -7`

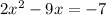
Step 3:

Find square of half of b

`((b)/(2))^2 =( (-9)/(2))^2`

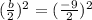
Add the term to each side of equation

`2x^2 - 9x + ((-9)/(2))^2= -7 + ((-9)/(2))^2`

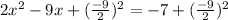
Simplify

`2x^2 - 9x + ((9)/(2))^2= -7 + (81)/(4)\\\\2x^2 - 9x + ((9)/(2))^2= (53)/(4)`

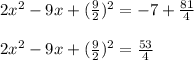
The left side is of form:

`(a-b)^2 = a^2 - 2ab + b^2`

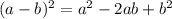
Therefore,

`(2x + 9)^2 = (53)/(4)`

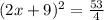
Thus the solution is found