There are 189 bacteria in 5 hours
There are 13382588 bacteria in 1 day
There are
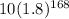 bacteria in 1 week
bacteria in 1 week
Solution:
Given that,
A type of bacteria has a very high exponential growth rate of 80% every hour
There are 10 bacteria
The increasing function is given as:
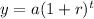
Where,
y is future value
a is initial value
r is growth rate
t is time period
From given,
a = 10
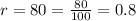
Determine how many will be in 5 hours
Substitute t = 5
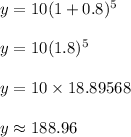
y = 189
Thus, there are 189 bacteria in 5 hours
Determine how many will be in 1 day ?
1 day = 24 hours
Substitute t = 24

Thus, there are 13382588 bacteria in 1 day
Determine how many will be in 1 week
1 week = 168
Substitute t = 168
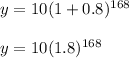
Thus there are
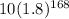 bacteria in 1 week
bacteria in 1 week