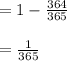Answer:
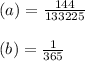
Explanation:
Part (a) the probability that two people have a birthday on the 9th of any month.
Neglecting leap year, there are 365 days in a year.
There are 12 possible 9th in months that make a year calendar.
If two people have birthday on 9th; P(1st person) and P(2nd person).

Part (b) the probability that two people have a birthday on the same day of the same month
P(2 people selected have birthday on the same day of same month) + P(2 people selected not having birthday on same day of same month) = 1
P(2 people selected not having birthday on same day of same month):
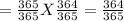
P(2 people selected have birthday on the same day of same month)