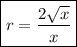Step-by-step explanation:
See the figure below for a better understanding of the problem. Since we have a 45-45-90 triangle, this is an isosceles triangle, so both the adjacent and opposite sides measure the same value, say, x. Then the hypotenuse would be:
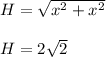
Then. the ratio of the length of the hypotenuse to the length of a side is: