Question

Solve for X, and graph
8. - 6x + 14 <-28 OR 9x + 15 <- 12

Answer 1

For this case we must indicate the solution set of the given inequalities:

`-6x + 14 <-28`

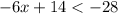
Subtracting 14 from both sides of the inequality we have:

`-6x <-28-14\\-6x <-42`

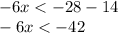
Dividing by 6 on both sides of the inequality:

`-x <- \frac {42} {6}\\-x <-7`

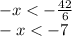
We multiply by -1 on both sides, taking into account that the sense of inequality changes:

`x> 7`

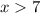
Thus, the solution is given by all values of x greater than 7.

On the other hand we have:

`9x + 15 <-12`

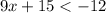
Subtracting 15 from both sides of the inequality we have:

`9x <-12-15\\9x <-27`

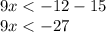
Dividing between 9 on both sides of the inequality we have:

`x <- \frac {27} {9}\\x <-3`

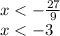
Thus, the solution is given by all values of x less than -3.

Finally, the solution set is:

(-∞, - 3) U (7,∞)

Answer:

(-∞, - 3) U (7,∞)