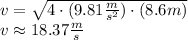Question

At what minimum speed must a roller coaster be traveling so that passen- gers upside down at the top of the circle (Fig. 5–48) do not fall out? Assume a radius of curvature of 8.6 m.

Answer 1

Answer:
`v \approx 18.37 (m)/(s)`

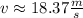
Step-by-step explanation:

Let assume that system is conservative. From application of the Principle of Energy Conservation, it is noticed that initial linear kinetic energy must be equal to the gravitational energy at the top of the circle. That is to say:

`K_(1) = U_(2)\\`

`(1)/(2) \cdot m \cdot v^(2) = m \cdot g \cdot (2\cdot R) \\v = √(4 \cdot g \cdot R)`

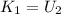
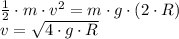
Where
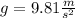`g = 9.81 (m)/(s^(2))`.

`v = \sqrt{4 \cdot (9.81 (m)/(s^2))\cdot(8.6 m)} \\v \approx 18.37 (m)/(s)`