Answer:
Correct option: (b) 32.357 and 71.420
Step-by-step explanation:
The confidence interval for population variance σ² is:
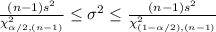
Given:
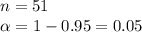
Compute the critical values of chi-square as follows:
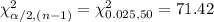
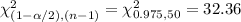
Use the chi-square table for the critical value.
Thus, the critical values are 32.36 and 71.42.