Question

If you are given the graph of h(x)=log6x, how could you graph m(x)=log6(x+3)?

Translate each point of the graph of h(x) 3 units up.
Translate each point of the graph of h(x) 3 units down.
Translate each point of the graph of h(x) 3 units right.
Translate each point of the graph of h(x) 3 units left.

Answer 1

Answer: last option.

Explanation:

There are several transformations for a function f(x). Some of them are shown below:

1. If
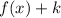`f(x)+k`, then the function is translated "k" units up.

2. If
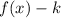`f(x)-k`, then the function is translated "k" units down.

3. If
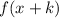`f(x+k)`, then the function is translated "k" units left.

4. If
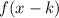`f(x-k)`, then the function is translated "k" units right.

In this case you have the following function:

`h(x)=log_6x`

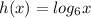
And the function m(x) is obtained by transformating the function h(x). This function is:

`m(x)=log_6(x+3)`

Then, based on the transformatios shown before, you can identify that:

`m(x)=h(x+3)`

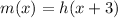
Therefore, you can determine that you could graph the function
`m(x)=log_6(x+3)` by translating each point of the graph of the function h(x) 3 units left.