Question

Solve for X
1. - 6x + 14 < =28 OR
9x + 15 <-12

Answer 1

1)

`-6x + 14\leq 28`

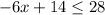
Solve the inequality for "x"

From given,

`-6x + 14\leq 28`

`\mathrm{Subtract\:}14\mathrm{\:from\:both\:sides}\\\\-6x+14-14\le \:28-14\\\\Simplify\\\\-6x\le \:14\\\\\mathrm{Multiply\:both\:sides\:by\:-1\:\left(reverse\:the\:inequality\right)}`

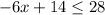
When, we multiply or divide both sides of inequality by negative number, then we must flip the inequality sign

`\left(-6x\right)\left(-1\right)\ge \:14\left(-1\right)\\\\\mathrm{Simplify}\\\\6x\ge \:-14\\\\\mathrm{Divide\:both\:sides\:by\:}6\\\\(6x)/(6)\ge (-14)/(6)\\\\x \geq -2.333`

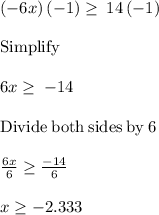
The solution set is given as:

`-6x+14\le \:28\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x\ge \:-(7)/(3)\:\\ \:\mathrm{Decimal:}&\:x\ge \:-2.33333\dots \\ \:\mathrm{Interval\:Notation:}&\:[-(7)/(3),\:\infty \:)\end{bmatrix}`

---------------------------------------------------------------------------------------------------

2)

`9x + 15< - 12`

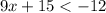
Solve the inequality for "x"

From given,

`9x+15<-12\\\\\mathrm{Subtract\:}15\mathrm{\:from\:both\:sides}\\\\9x+15-15<-12-15\\\\\mathrm{Simplify}\\\\9x<-27\\\\\mathrm{Divide\:both\:sides\:by\:}9\\\\(9x)/(9)<(-27)/(9)\\\\\mathrm{Simplify}\\\\x < -3`

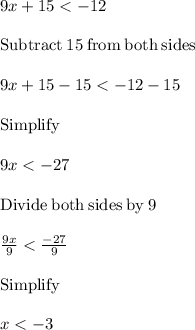
The solution set is given as:

`9x+15<-12\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-3\right)\end{bmatrix}`