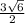Question

Pls help asap, have a great day

find, w: x: y: z:

Answer 1

See below ↓

Explanation:

Finding w and x [both are equal]

• Take the cos function of one of the 45° angles, which is the ratio of the adjacent side to the hypotenuse
• cos(45°) =
  `(1)/(√(2) ) = (w)/(6)`
• ⇒ w =
  `(6)/(√(2) ) = (6)/(√(2) ) *(√(2) )/(√(2) ) = (6√(2) )/(2)`
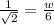
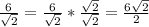
• ⇒ w = 3√2 and x = 3√2

Finding y

• Take the cos ratio of the 60° angle to find y
• cos(60°) =
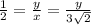
  `(1)/(2) = (y)/(x) = (y)/(3√(2) )`
• ⇒ y =
  `(3√(2) )/(2)`

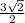
Finding z

• Take the sin ratio of 60° angle of the triangle, which is the ratio of the opposite side to the hypotenuse
• sin(60°) =
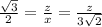
  `(√(3) )/(2)= (z)/(x) = (z)/(3√(2) )`
• ⇒ z =
  `(3√(6) )/(2)`