Question

In 1958, a first-class postage stamp for a 1-ounce envelope was $0.04. In 2012, a first-class postage stamp for the same envelope is $0.45. What was the annual compound increase in the cost of the first-class postage during the 54 year period

Answer 1

The annual increase was approximately $0.002

Step-by-step explanation:

In order to know the annual compound increase in the cost of the first-class postage during the 54 year period, we need to know the rate at which the compound interest was calculated. We can know that using the following compound interest formula:

`A = P(1 + (r)/(100))^(t)`

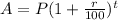
P = principal amount (the initial amount for the envelope)

r = annual rate of increase

t = number of years the amount is increased.

A = amount of money accumulated after n years, including the increase.

Now, we have our Amount at the 54th year to be 0.45dollars, when the principal is 0.04dollars.

Therefore, we have

A = $0.45

P = $0.04

r = unknown (that's what we are looking for)

t = 54

Substituting these into the formula, we have:

`0.45 = 0.04(1 + (r)/(100))^(54)`

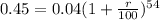
Dividing both sides by 0.04 we have:

`11.25 = (1 + (r)/(100))^(54)`

Taking the 54th root of both sides we have(approximately):

`1.05 = (1 + (r)/(100))`

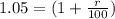
The above gives:

`0.05 = (r)/(100)`

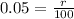
This gives:

`r = 5%`

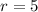
Therefore, the money increased annually at the rate of 5% approximately, and that would be

`(5)/(100) * 0.04`

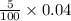
Which is $0.002 approximately.