Question

You have a battery marked " 6.00 V ." When you draw a current of 0.361 A from it, the potential difference between its terminals is 5.07 V . What is the potential difference when you draw 0.591 A

Answer 1

V = 4.48 V

Step-by-step explanation:

• As the potential difference between the battery terminals, is less than the rated value of the battery, this means that there is some loss in the internal resistance of the battery.

• We can calculate this loss, applying Ohm's law to the internal resistance, as follows:

`V_(rint) = I* r_(int)`

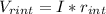
• The value of the potential difference between the terminals of the battery, is just the voltage of the battery, minus the loss in the internal resistance, as follows:

`V = V_(b) - V_(rint) = 5.07 V = 6.00 V - 0.361 A * r_(int)`

• We can solve for rint, as follows:

`r_(int) =(V_(b)- V_(rint) )/(I) = (6.00 V - 5.07 V)/(0.361A) = 2.58 \Omega`

• When the circuit draws from battery a current I of 0.591A, we can find the potential difference between the terminals of the battery, as follows:

`V = V_(b) - V_(rint) = 6.00 V - 0.591 A * 2.58 \Omega = 4.48 V`

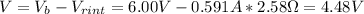
• As the current draw is larger, the loss in the internal resistance will be larger too, so the potential difference between the terminals of the battery will be lower.

Answer 2

Step-by-step explanation:

Battery voltage is 6V

A current of 0.361A is draw the voltage reduces to, 5.07V

This shows that the appliances resistance that draws the currents is

Using KVL

The battery has an internal resistance r

V=Vr+Va

Vr is internal resistance voltage

Va is appliance voltage

6=5.07+Va

Va=6-5.07

Va=0.93

Using ohms law to the resistance of the appliance

Va=iR

R=Va/i

R=0.93/0.361

R=2.58ohms

Then if the circuit draws a current of 0.591A

Then the voltage across the load is

V=iR

Va=0.591×2.58

Va=1.52V

Then the voltage drop at the internal resistance is

V=Vr+Va

Vr=V-Va

Vr=6-1.52

Vr=4.48V