Answer:
Width = 25
Length = 25
Area = 625
Explanation:
The perimeter of a rectangle is given by the sum of its four sides (2L+2W) while the area is given by the product of the its length by its width (LW). It is possible to write the area as a function of width as follows:
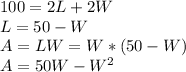
The value of W for which the derivate of the area function is zero is the width that yields the maximum area:
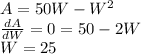
With the value of the width, the length (L) and the area (A) can be also be found:
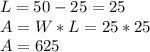
Since the values satisfy the condition W≤L, the answer is:
Width = 25
Length = 25
Area = 625