Answer:
a) P ( 3 ≤X≤ 5 ) = 0.02619
b) E(X) = 1
Explanation:
Given:
- The CDF of a random variable X = { 0 , 1 , 2 , 3 , .... } is given as:
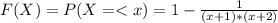
Find:
a.Calculate the probability that 3 ≤X≤ 5
b) Find the expected value of X, E(X), using the fact that. (Hint: You will have to evaluate an infinite sum, but that will be easy to do if you notice that
Solution:
- The CDF gives the probability of (X < x) for any value of x. So to compute the P ( 3 ≤X≤ 5 ) we will set the limits.
![F(X) = P ( 3=<X =< 5) = [1 - (1)/((x+1)*(x+2))]\limits^5_3\\\\F(X) = P ( 3=<X =< 5) = [-(1)/((5+1)*(5+2)) + (1)/((3+1)*(3+2))}\\\\F(X) = P ( 3=<X =< 5) = [-(1)/((42)) + (1)/((20))}]\\\\F(X) = P ( 3=<X =< 5) = 0.02619](https://img.qammunity.org/2021/formulas/mathematics/college/sazrls14q1bmi7q0kwflindda4zmmfn7l6.png)
- The Expected Value can be determined by sum to infinity of CDF:
E(X) = Σ ( 1 - F(X) )
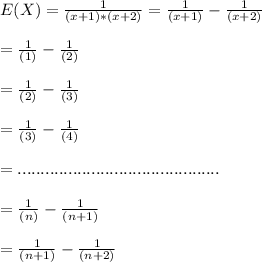
E(X) = Limit n->∞ [1 - 1 / ( n + 2 ) ]
E(X) = 1