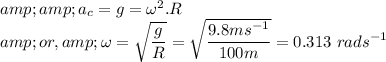Question

A rotating space station is said to create "artificial gravity"—a loosely-defined term used for an acceleration that would be crudely similar to gravity. The outer wall of the rotating space station would become a floor for the astronauts, and centripetal acceleration supplied by the floor would allow astronauts to exercise and maintain muscle and bone strength more naturally than in non-rotating space environments.If the space station is 200 m in diameter, what angular velocity would produce an "artificial gravity" of 9.80 m/s2 at the rim?

Answer 1

The required angular velocity (ω) will be
`0.313~rads^(-1)`.

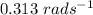Step-by-step explanation:

Due to the rotation of the space station the astronauts experience a centripetal acceleration towards the centre of the space station. If '
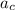`\large{a_(c)}`', 'ω' and 'R' represent the centripetal acceleration, angular velocity of the space station and the radius of the space station respectively, then

`a_(c) = \omega^(2).R`

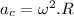
As according to the problem the space station has to rotate in such an angular velocity that it produces the same "artificial gravity" as Earth's surface, we can write

`a_(c) = g = 9.8 ms^(-2)`

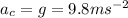
Also given
`R = (diameter~of~the~space~station)/(2) = (200 m)/(2) = 100 m`

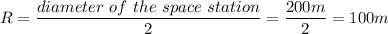
Therefore we can write,

`&& a_(c) = g = \omega^(2).R\\&or,& \omega = \sqrt{(g)/(R)} = \sqrt{(9.8 ms^(-1))/(100 m)} = 0.313~rads^(-1)`