Question

A market research firm knows from historical data that telephone surveys have a 36% response rate. In a random sample of 280 telephone numbers, what is the probability that the response rate will be between 33.5% and 39%?

Answer 1

Probability that the response rate will be between 33.5% and 39% = 0.66176 .

Explanation:

We are given that a market research firm knows from historical data that telephone surveys have a 36% response rate.

The probability criterion we will use here is;

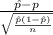`\frac{\hat p- p}{\sqrt{(\hat p (1-\hat p))/(n) } }` ~ N(0,1)

Here, p = 0.36 and n = sample size = 280

Let
`\hat p` = response rate

So, P(0.335 <=
`\hat p` <= 0.39) = P(
`\hat p` <= 0.39) - P(
`\hat p` < 0.335)

P(
`\hat p` <= 0.39) = P(
`\frac{\hat p- p}{\sqrt{(\hat p (1-\hat p))/(n) } }` <=
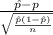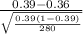`\frac{0.39- 0.36}{\sqrt{(0.39 (1-0.39))/(280) } }` ) = P(Z <= 1.03) = 0.84849

P(
`\hat p` < 0.335) = P(
`\frac{\hat p- p}{\sqrt{(\hat p (1-\hat p))/(n) } }` <
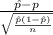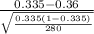`\frac{0.335- 0.36}{\sqrt{(0.335 (1-0.335))/(280) } }` ) = P(Z < -0.89) = 1 - P(Z <= 0.89)

= 1 - 0.81327 = 0.18673

Therefore, P(0.335 <=
`\hat p` <= 0.39) = 0.84849 - 0.18673 = 0.66176

Hence, probability that the response rate will be between 33.5% and 39% is 0.66176 or 66.18 % .

Answer 2

0.6604

Explanation:

Given that a market research firm knows from historical data that telephone surveys have a 36% response rate.

Sample size of random sample = 280

We know for samples randomly drawn of large size sample proportion follows a normal distribution with mean= sample proportin and std error

=
`\sqrt{(pq)/(n) }`

Substitute p = 0.36 and q = 1-0.36= 0.64

p follows N with mean = 0.36 and std dev =
`\sqrt{(0.36*0.64)/(√(280) ) } \\=0.0287`

Using normal distribution values we can find\

`P(33.5p.c. < p < 39pc)\\= P(0.335<p<0.39)\\= F(0.39)-F(0.335)\\= 0.852183-0.191735\\=0.660448`