Question

Chase consumes an energy drink that contains caffeine. After consuming the energy drink, the amount of caffeine in Chase's body decreases exponentially. The 10-hour decay factor for the number of mg of caffeine in Chase's body is 0.2542. a. What is the 5-hour growth/decay factor for the number of mg of caffeine in Chase's body? b. What is the 1-hour growth/decay factor for the number of mg of caffeine in Chase's body?c. If there were 171 mg of caffeine in Chase's body 1.39 hours after consuming the energy drink, how many mg of caffeine is in Chase's body 2.39 hours after consuming the energy drink?

Answer 1

The 5-hour growth/decay factor is 0.561, the 1-hour growth/decay factor is 0.869, and there are 154 mg of caffeine in Chase's body 2.39 hours after consuming the energy drink.

Step-by-step explanation:

a. To find the 5-hour growth/decay factor, we raise the 10-hour decay factor to the power of (5/10). So, the 5-hour growth/decay factor is 0.2542^(5/10) = 0.561.

b. To find the 1-hour growth/decay factor, we raise the 10-hour decay factor to the power of (1/10). So, the 1-hour growth/decay factor is 0.2542^(1/10) = 0.869.

c. To find the number of mg of caffeine in Chase's body 2.39 hours after consuming the energy drink, we multiply the initial amount of caffeine by the 2.39-hour decay factor. So, the number of mg is 171 * 0.2542^(2.39/10) = 154.

Answer 2

(a) The 5-hour decay factor is 0.5042.

(b) The 1-hour decay factor is 0.8720.

(c) The amount of caffeine in Chase's body 2.39 hours after consuming the drink is 149.112 mg.

Step-by-step explanation:

The amount of caffeine in Chase's body decreases exponentially.

The 10-hour decay factor for the number of mg of caffeine is 0.2542.

The 1-hour decay factor is:

`1-hour\ decay\ factor=(0.2542)^(1/10)=0.8720`

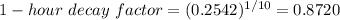
(a)

Compute the 5-hour decay factor as follows:

`5-hour\ decay\ factor=(0.8720)^(5)\\=0.504176\\\approx0.5042`

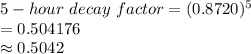
Thus, the 5-hour decay factor is 0.5042.

(b)

The 1-hour decay factor is:

`1-hour\ decay\ factor=(0.2542)^(1/10)=0.8720`

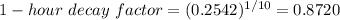
Thus, the 1-hour decay factor is 0.8720.

(c)

The equation to compute the amount of caffeine in Chase's body is:

A = Initial amount × (0.8720)ⁿ

It is provided that initially Chase had 171 mg of caffeine, 1.39 hours after consuming the drink.

Compute the amount of caffeine in Chase's body 2.39 hours after consuming the drink as follows:

`A = Initial\ amount * (0.8720)^(2.39) \\=[Initial\ amount * (0.8720)^(1.39)] *(0.8720)\\=171* 0.8720\\=149.112`

Thus, the amount of caffeine in Chase's body 2.39 hours after consuming the drink is 149.112 mg.