Question

The velocity of a sky diver t seconds after jumping is given by v(t) = 80(1 − e−0.2t). After how many seconds is the velocity 65 ft/s? (Round your answer to the nearest whole number.)

Answer 1

8 seconds

Step-by-step explanation:

Given:

The velocity of the sky diver 't' seconds after jumping is given as:

`v(t)=80(1-e^(-0.2t))`

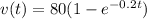
The velocity is given as,
`v=65\ ft/s`

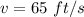
So, in order to find the time required to reach the above given velocity, we plug in 65 for 'v' in the above equation and solve for time 't'. This gives,

`65=80(1-e^(-0.2t))\\\\(65)/(80)=1-e^(-0.2t)\\\\0.8125=1-e^(-0.2t)\\\\e^(-0.2t)=1-0.8125\\\\\textrm{Taking natural log on both sides, we get:}\\\\-0.2t=\ln(0.1875)\\\\t=(\ln(0.1875))/(-0.2)\\\\t=8.4\ s\approx 8\ s(Nearest\ whole\ number)`

Therefore, the time taken to reach a velocity of 65 ft/s is nearly 8 seconds.