Question

car leaves a stop sign and exhibits a constant acceleration of 0.300 m/s2 parallel to the roadway. The car passes over a rise in the roadway such that the top of the rise is shaped like an arc of a circle of radius 500 m. Now the car is at the top of the rise, its velocity vector is horizontal and has a magnitude of 6.00 m/s. What are the magnitude and direction of the total acceleration vector for the car at this instant

Answer 1

0.308 m/s2 at an angle of 13.5° below the horizontal

Step-by-step explanation:

The parallel acceleration to the roadway is the tangential acceleration on the rise.

The normal acceleration is the centripetal acceleration due to the arc. This is given by

`a_N = (v^2)/(r) = (36^2)/(500)=0.072`

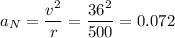
The tangential acceleration, from the question, is

`a_T = 0.300`

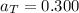
The magnitude of the total acceleration is the resultant of the two accelerations. Because these are perpendicular to each other, the resultant is given by

`a^2 =a_T^2 + a_N^2 = 0.300^2 + 0.072^2`

`a = 0.308`

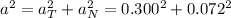
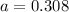
The angle the resultant makes with the horizontal is given by

`\tan\theta=(a_N)/(a_T)=(0.072)/(0.300)=0.2400`

`\theta=13.5`

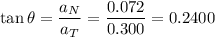
Note that this angle is measured from the horizontal downwards because the centripetal acceleration is directed towards the centre of the arc