Question

According to Scarborough Research, more than 85% of working adults commute by car. Of all U.S. cities, Washington, D.C., and New York City have the longest commute times. A sample of 25 commuters in the Washington, D.C., area yielded the sample mean commute time of 27.97 minutes and sample standard deviation of 10.04 minutes. Construct and interpret a 99% confidence interval for the mean commute time of all commuters in Washington D.C. area.

Answer 1

The 99% confidence interval for the mean commute time of all commuters in Washington D.C. area is (22.35, 33.59).

Explanation:

The (1 - α) % confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha /2)(\sigma)/(√(n))`

Here the population standard deviation (σ) is not provided. So the confidence interval would be computed using the t-distribution.

The (1 - α) % confidence interval for population mean (μ) using the t-distribution is:

`CI=\bar x\pm t_(\alpha /2,(n-1))(s)/(√(n))`

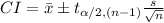
Given:

`\bar x=27.97\\s=10.04\\n=25\\t_(\alpha /2, (n-1))=t_(0.01/2, (25-1))=t_(0.005, 24)=2.797`

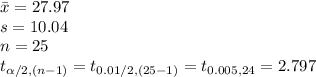
*Use the t-table for the critical value.

Compute the 99% confidence interval as follows:

`CI=27.97\pm 2.797*(10.04)/(√(25))\\=27.97\pm5.616\\=(22.354, 33.586)\\\approx(22.35, 33.59)`

Thus, the 99% confidence interval for the mean commute time of all commuters in Washington D.C. area is (22.35, 33.59).