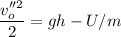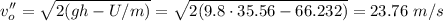Question

A particle is uncharged and is thrown vertically upward from ground level with a speed of 26.4 m/s. As a result, it attains a maximum height h. The particle is then given a positive charge +q and reaches the same maximum height h when thrown vertically upward with a speed of 28.8 m/s. The electric potential at the height h exceeds the electric potential at ground level. Finally, the particle is given a negative charge -q. Ignoring air resistance, determine the speed with which the negatively charged particle must be thrown vertically upward, so that it attains exactly the maximum height h. In all three situations, be sure to include the effect of gravity.

Answer 1

`23.76 \ m/s`

Step-by-step explanation:

Energy Conversions

This is an example where the mechanical energy is not conserved since an external force is acting and distorting the original balance between kinetic and potential gravitational energy.

Let's start with the first event, the particle being thrown upwards with an initial speed vo. The initial mechanical energy at zero height is only kinetic:

`\displaystyle M=(mv_o^2)/(2)`

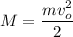
When the particle reaches its maximum height, the mechanical energy is only potential gravitational:

M'=mgh

Equating both:

`\displaystyle (mv_o^2)/(2)=mgh`

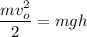
Simplifying by m and solving for h

`\displaystyle h=(v_o^2)/(2g)=(26.4^2)/(2\cdot 9.8)=35.56\ m`

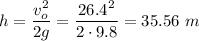
The particle is then given a positive charge and we know it reaches the same maximum height when the initial speed is 28.8 m/s. The initial kinetic energy was not totally converted to potential gravitational energy. The charge that was given to the particle and the electric potential present changed the energy balance by introducing a new member into the equation. The final energy at maximum height is

`M'=mgh+U`

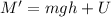
Where U is the electric energy the particle has when reached the maximum height. Equating the initial and final energies we have

`\displaystyle (mv_o'^2)/(2)=mgh+U`

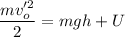
Simplifying by m and solving for U

`\displaystyle U/m=(v_o'^2)/(2)-gh=(28.8^2)/(2)-9.8\cdot 35.56`

`U/m=66.232\ J/Kg`

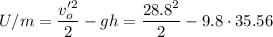
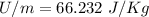
This energy makes the particle have an additional force downwards that brakes it until it stops. When the charge is negative, the new electrical force will be directed upwards in such a way that the particle will reach the same maximum height with less initial speed v''o. The new equilibrium equation will be

`\displaystyle (mv_o''^2)/(2)=mgh-U`

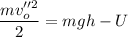
Simplifying by m and solving for v''o

`\displaystyle (v_o''^2)/(2)=gh-U/m`

`\displaystyle v_o''=√(2(gh-U/m))=√(2(9.8\cdot 35.56 -66.232))=23.76\ m/s`

`\boxed{v_o''=23.76 \ m/s}`