Question

The slit-to-screen distance is D = 200 cm , and the laser wavelength is 633 nm, use the formula for single-slit diffraction minima to find the slit width a.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The slit width
`a = (2L \lambda)/(W)`

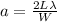
Step-by-step explanation:

Assuming the unit on the graph is cm

Given that the slit to screen distance is D = 200 cm = 20 000 m

The wavelength
`\lambda` = 633 nm =
`633*10^(-9)m`

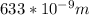
slit width a = ?

The width of the spot that is the width of the peak from the graph is

W = 1.6 × 2 = 3.2 cm

Where the 1.6 is the distance from 0 to the right end point of the peak

The change in y i.e
`\Delta y` has a formula

`\Delta y` = Ltanθ

An the width of the spot is 2 ×
`\Delta y`

W = 2Ltanθ

Applying this formula qsinθ = m
`\lambda`

where m = 1 because we a focused on the first zeros ,using small angle approximation we have y

`a\theta = (1) \lambda`

`\theta = (\lambda)/(a)`

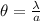
Substituting this into W = 2ltanθ

Using small angle approximation

W = 2ltanθ = 2Lθ

`W = 2L(\lambda)/(a)`

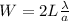
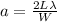`a = (2L \lambda)/(W)` and this is the slit width