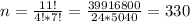Question

Seven blue and four red balls are to be arranged in order. How many ways can this be done if (1) The blue balls are distinguishable (e.g. numbered) as are the red balls. (2) Blue balls are distinguishable, but the red balls are identical. (3) The balls of each color are indistinguishable.

Answer 1

1) n = 39916800

2) n = 1663200

3) n = 330

Explanation:

1) If the blue balls are distinguishable as are the red balls

Then you can arrange these balls in the following ways, we must use a permutation

In totally we have 11 balls, then

n = 11P11

`n = (11!)/((11-11)!) = 11! = 39916800\\`

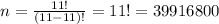
2) If Blue balls are distinguishable, but the red balls are identical

In this case, we need to do a correction due to the red balls are identical and we cannot identify the difference when we interchange two red balls

`n = (11!)/(4!) = (39916800)/(24) = 1663200`

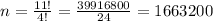
3) If the balls of each color are indistinguishable

We proceed equal to the before case but we include a correction due to blue balls also

`n = (11!)/(4!*7!) = (39916800)/(24*5040) = 330`