Answer:
The force developed in the link is 6.36 N.
Step-by-step explanation:
Given that,
Mass of block A = 10 kg
Mass of block B = 6 kg
Coefficients of kinetic friction
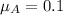
Coefficients of kinetic friction
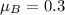
Suppose the angle is 30°
We need to calculate the acceleration
Using formula of acceleration
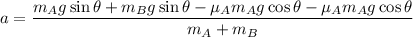
Put the value into the formula
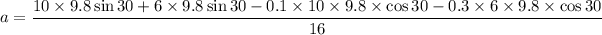
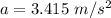
We need to calculate the force developed in the link
For block A,
Using balance equation

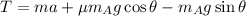
Put the value into the formula
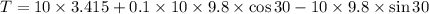
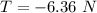
Negative sign shows the opposite direction of the force.
Hence, The force developed in the link is 6.36 N.