Step-by-step explanation:
The given data is as follows.
Dielectric constant, K = 3.0
Area of the plates (A) = 0.021

Distance between plates (d) =
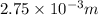
Maximum electric field (E) =
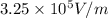
Now, we will calculate the capacitance as follows.
C =
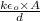
=
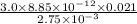
=
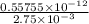
=
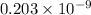 F
F
Formula to calculate electric charge is as follows.
E =
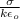
or, Q =
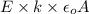 (as
(as
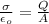 )
)
=
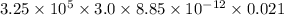
=
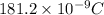
Formula to calculate the energy is as follows.
U =
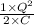
=
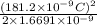
=
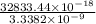
=

or, =

Thus, we can conclude that the maximum energy that can be stored in the capacitor is
 .
.