Answer:
The value of
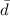 is -0.2.
is -0.2.
The value of
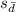 is 0.3464.
is 0.3464.
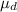 = mean difference in body temperatures.
= mean difference in body temperatures.
Explanation:
The data for body temperatures from five different subjects measured at 8 AM and again at 12 AM are provided.
The formula of
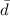 and
and
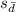 are:
are:
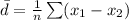
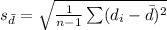
Consider the table below.
Compute the value of
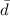 as follows:
as follows:

Thus, the value of
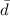 is -0.2.
is -0.2.
Compute the value of
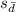 as follows:
as follows:
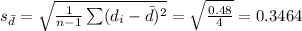
Thus, the value of
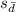 is 0.3464.
is 0.3464.
The variable
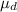 represents the mean difference in body temperatures measured at 8 AM and again at 12 AM.
represents the mean difference in body temperatures measured at 8 AM and again at 12 AM.