Question

During a very quick stop, a car decelerates at 6.2 m/s2. Assume the forward motion of the car corresponds to a positive direction for the rotation of the tires (and that they do not slip on the pavement). Randomized Variables at = 6.2 m/s2 r = 0.275 m ω0 = 93 rad/s

a. What is the angular acceleration of its tires in rad/s2, assuming they have a radius of 0.275 m and do not slip on the pavement?
b. How many revolutions do the tires make before coming to rest, given their initial angular velocity is 93 rad/s ?
c. How long does the car take to stop completely in seconds?
d. What distance does the car travel in this time in meters?
e. What was the car’s initial speed in m/s?

Answer 1

a)
`-22.5 rad/s^2`

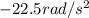
b) 30.6 revolutions

c) 4.13 s

d) 52.9 m

e) 25.6 m/s

Step-by-step explanation:

a)

The relationship between linear acceleration and angular acceleration for an object in circular motion is given by

`a=\alpha r`

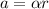
where

`a` is the linear acceleration

`\alpha` is the angular acceleration

r is the radius of the motion of the object

For the tires of the car in this problem, we have:

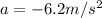`a=-6.2 m/s^2` is the linear acceleration (the car is slowing down, so it is a deceleration, therefore the negative sign)

r = 0.275 m is the radius of the tires

Solving for
`\alpha`, we find the angular acceleration:

`\alpha = (a)/(r)=(-6.2)/(0.275)=-22.5 rad/s^2`

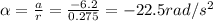
b)

To solve this part of the problem, we can use the suvat equation for the rotational motion, in particular:

`\omega^2 - \omega_0^2 = 2\alpha \theta`

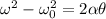
where:

`\omega` is the final angular velocity

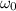`\omega_0` is the initial angular velocity

`\alpha` is the angular acceleration

`\theta` is the angular displacement

Here we have:

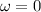`\omega=0` (the tires come to a stop)

`\omega_0 = 93 rad/s`

`\alpha = -22.5 rad/s^2`

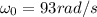
Solving for
`\theta`, we find the angular displacement:

`\theta=(\omega^2-\omega_0^2)/(2\alpha)=(0^2-(93)^2)/(2(-22.5))=192.2 rad`

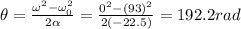
And since 1 revolution =
`2\pi rad`,

`\theta=(192.2)/(2\pi)=30.6 rev`

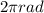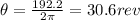
c)

To solve this part, we can use another suvat equation:

`\omega=\omega_0 + \alpha t`

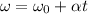
where in this case, we have:

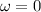`\omega=0` is the final angular velocity, since the tires come to a stop

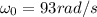`\omega_0 = 93 rad/s` is the initial angular velocity

`\alpha=-22.5 rad/s^2` is the angular acceleration

t is the time

Solving for t, we can find the time required for the tires (and the car) to sopt:

`t=(\omega-\omega_0)/(\alpha)=(0-93)/(-22.5)=4.13 s`

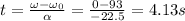
d)

The car travels with a uniformly accelerated motion, so we can find the distance it covers by using the suvat equations for linear motion:

`s=vt-(1)/(2)at^2`

where:

v = 0 is the final velocity of the car (zero since it comes to a stop)

t = 4.13 s is the time taken for the car to stop

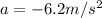`a=-6.2 m/s^2` is the deceleration for the car

s is the distance covered during this motion

Therefore, substituting all values and calculating s, we find the distance covered:

`s=0-(1)/(2)(-6.2)(4.13)^2=52.9 m`

e)

The relationship between angular velocity and linear velocity for a rotational motion is given by

`v=\omega r`

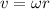
where

v is the linear velocity

`\omega` is the angular speed

r is the radius of the circular motion

In this problem:

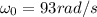`\omega_0 = 93 rad/s` is the initial angular speed of the tires

r = 0.275 m is the radius of the tires

Therefore, the initial velocity of the car is:

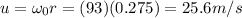`u=\omega_0 r = (93)(0.275)=25.6 m/s` is the initial velocity of the car