Question

A point charge of -3.0X10-5 C is placed at the origin of coordinates in vacuum. Find the electric field at the point x= 5.0 m on the x axis. Determine the acceleration of a proton (q=+e, m=1.67X10-27 kg) immersed in an electric field of strength 0.50 kN/C in vacuum. How many times greater is this acceleration than that due to gravity?

Answer 1

a) -10,800 N/C

b)
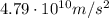
`4.79\cdot 10^(10)m/s^2`

c)
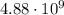`4.88\cdot 10^9` times g

Step-by-step explanation:

a)

The magnitude of the electric field produced by a single-point charge is given by

`E=(kQ)/(r^2)`

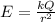
where

k is the Coulomb's constant

Q is the charge producing the field

r is the distance at which the field is calculated

In this problem:

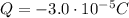`Q=-3.0\cdot 10^(-5)C` is the c harge producing the field

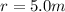`r=5.0 m` is the distance at which we want to calculate the field

Substituting,

`E=((9.0\cdot 10^9)(-3.0\cdot 10^(-5)))/((5.0)^2)=-10,800 N/C`

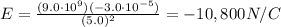
where the negative sign indicates that the direction of the field is towards the charge producing the field (for a negative charge, the electric field is inward, towards the charge)

b)

The force experienced by a charged particle in an electric field is given by

`F=qE`

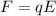
where

q is the magnitude of the charge

E is the electric field

Moreover, the force on an object can be written as:

`F=ma`

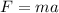
where

m is the mass

a is the acceleration

Combining the two equations,

`ma=qE\\a=(qE)/(m)`

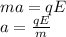
In this problem:

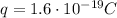`q=1.6\cdot 10^(-19)C` is the charge of the proton

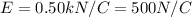`E=0.50 kN/C=500 N/C` is the strength of the electric field

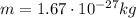`m=1.67\cdot 10^(-27) kg` is the mass of the proton

Substituting, we find the acceleration of the proton:

`a=((1.6\cdot 10^(-19))(500))/((1.67\cdot 10^(-27)))=4.79\cdot 10^(10)m/s^2`

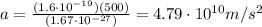
c)

The acceleration due to gravity is the acceleration at which every object near the Earth's surface falls down, in absence of air resistance, and it is given by

`g=9.81 m/s^2`

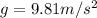
On the other hand, the acceleration of the proton in this problem is:

`a=4.79\cdot 10^(10) m/s^2`

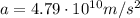
To find how many times greater is this acceleration than that due to gravity, we can divide the acceleration of the proton by the value of g. Doing so, we find:

`(a)/(g)=(4.79\cdot 10^(10))/(9.81)=4.88\cdot 10^9`

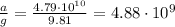
So, it is
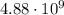`4.88\cdot 10^9` times greater than g.