Option A:
 is the solution of x
is the solution of x
Step-by-step explanation:
The given expression is
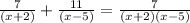
We need to determine the value of x.
The value of x can be determined by solving the expression for x.
Taking LCM , we get,
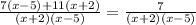
Since, the denominator is common for both sides of the equation, let us cancel the denominator.
Thus, we have,
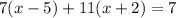
Multiplying the terms within the bracket, we get,
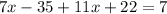
Adding the like terms, we get,
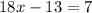
Adding both sides of the equation by 13, we have,
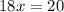
Dividing both sides of the equation by 18,
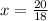
Simplifying, we get,

Thus, the solution is

Therefore, Option A is the correct answer.