Question

A satellite is in a circular orbit very close to the surface of a spherical planet. The period of the orbit is 2.17 hours. What is density of the planet

Answer 1

Step-by-step explanation:

Lets consider

Circumference of orbit = T

as it is mentioned in the question that a satellite is in orbit that is very close to the surface of planet. so

circumference of orbit = circumference of planet

Time period = T

radius of planet = R

orbital velocity = V

gravitational constant = G

mass of planet = m

Solution:

Time period for a uniform circular motion of orbit is,

T =
`(2\pi R)/(V)`

`T = \frac{2\pi R }{\sqrt{(GM)/(R) } }`

`T= 2\pi \sqrt{((R^3)/(GM) )}`

`M = (4)/(3) \pi R^(3)p`

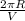
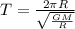
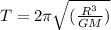
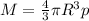
where p = density

`T = 2\pi \sqrt{(R^(3) )/(G(4)/(3)\pi R^(3) p ) }`

`T = \sqrt{(3\pi )/(Gp) }`

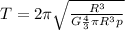
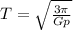
T = 2.17 hours = 7812 sec

(7812)² = [( 3×3.14)/6.67×
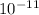`10^(-11)`×ρ)]

ρ = 6.28/6.67×
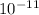`10^(-11)`×6.10×
`10^(-7)`

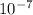
ρ = 6.28/40.687×
`10^(-18)`

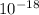
ρ = 0.1543×
`10^(18)`kg/m³

ρ = 15.43×
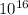`10^(16)`kg/m³